Among their extraordinary features, living systems balance the seemingly contradictory requirements of robustness, which entails a return to a stable state, and flexibility, which requires a family of states matched to external inputs. How these properties arise from inanimate matter is one of the leading questions faced by contemporary physicists: how can we describe life as a state of matter, and when does it arise? In my research I study this in the context of chemical reaction networks, having in mind Darwin’s ‘warm little pond’ that presumably led, by some unknown sequence of events, to all life on Earth today.
The surprising result of my research is that it is crucial that the component parts of life are small. Specifically, the chemical species cannot have too large a number of molecules. The reason is that large chemical reaction networks are too stable: they are robust, but they cannot jump between a variety of states, and therefore are inflexible. This result does not depend on the details of reactions, but only on fundamental physical laws (1).
In contrast, when the number of molecules is small, it is possible for systems to jump between different states, allowing flexibility. How such systems regain robustness is then a mystery.
Living matter must solve this robustness vs flexibility dilemma.
In contrast, when the number of molecules is small, it is possible for systems to jump between different states, allowing flexibility. How such systems regain robustness is then a mystery.
Living matter must solve this robustness vs flexibility dilemma.
 ‘liquid circuit,’ Calian. 2023.
‘liquid circuit,’ Calian. 2023.These considerations motivate Calian. A simulation of so-called reaction-diffusion dynamics (2) would generally lead to well-developed stable states, without flexibility. At the opposite extreme, cellular automata, which have a discrete, unsmooth dynamics, can host a great variety of patterns, but they are utterly unpredictable.
Calian walks the line between these extremes. The smooth dynamics of reaction-diffusion is subtlely broken in several distinct ways, each leading to new structures that are expressed across the Calian collection.
First, the dynamics is made sensitive to very small amounts of the competing chemical species. Coupled with the underlying discrete grid on which they live, this allows us to evade the aforementioned theorem that would restrict the dynamics. In other words, the simulation is not simply integration of differential equations.
Second, instead of simple diffusion -- smoothing out of inhomogeneities -- Calian allows both anti-diffusion, which leads to instabilities and therefore complexity, and anisotropic diffusion, that is diffusion that depends on the direction. This allows patterns that can have square or diamond edges, growth along cardinal directions, and other phenomena.
Third, the reactions are catalyzed by random nutrient fields that move across the canvas and evolve in time. Sometimes they lead to tornado-like vortices shearing the medium.


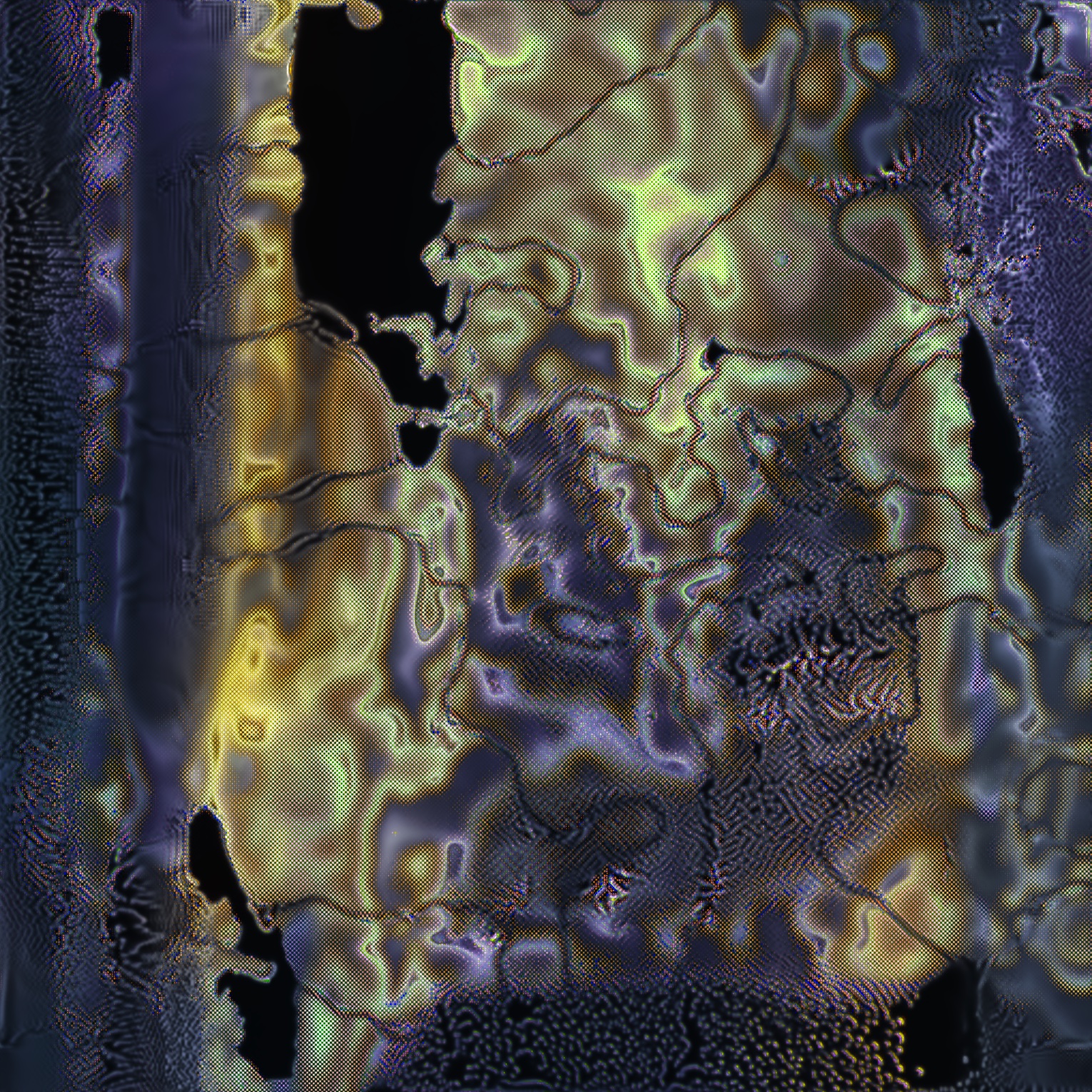
‘bouquet’
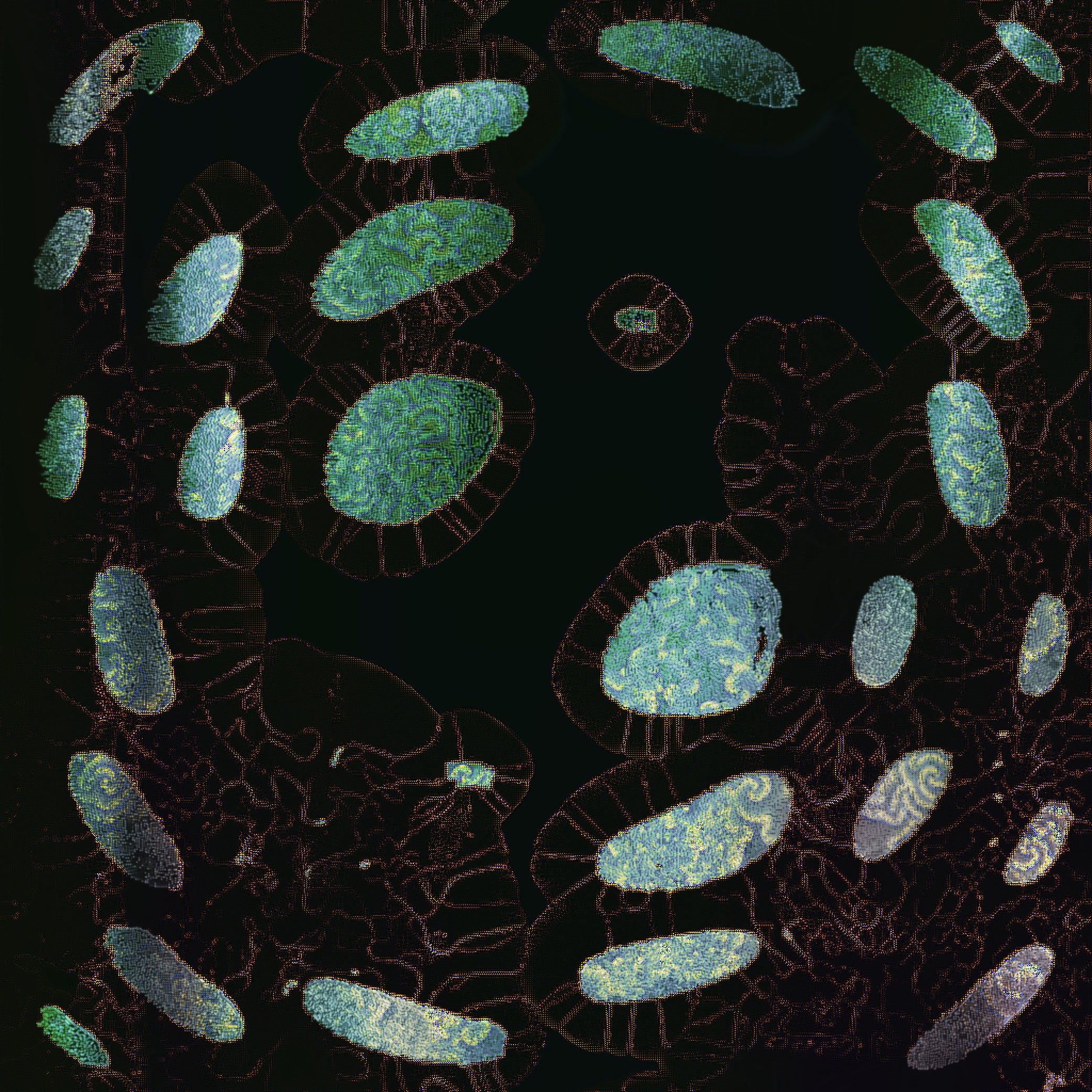
‘the forest path to the spring’
Altogether the key parameters controlling the dynamics span about 20 dimensions. Each style, of which there are 15, starts at a specific point in this 20 dimensional space, and is associated to a fixed palette. The styles have distinct personalities, variously highlighting or suppressing the features described above. Some styles, such as ‘constellation’ and ‘nocturne’, gently develop into detailed point-like structures; while others, like ‘bouquet’ and ‘the forest path to the spring’, dazzle with instability and growth. Some, like ‘kind of blue’ and ‘liquid circuit’, show explicitly the tension between organic and digital.
Species can either grow smoothly (’classical’) or in discrete jumps (’quantum’).
The aim of all these ingredients is to make Calian a dynamic complex system that evolves eternally and can be explored at different scales (by zooming and panning). I encourage the viewer to spend time with each piece, both watching it develop in place, and seeing how the ecosystem reacts as you interact with it.
Is it alive? How do you decide?
Species can either grow smoothly (’classical’) or in discrete jumps (’quantum’).
The aim of all these ingredients is to make Calian a dynamic complex system that evolves eternally and can be explored at different scales (by zooming and panning). I encourage the viewer to spend time with each piece, both watching it develop in place, and seeing how the ecosystem reacts as you interact with it.
Is it alive? How do you decide?
(1) The technical result is that chemical reaction networks in the large-particle-number deterministic limit have a function that never increases in time ( a Lyapunov function ), so they cannot hop between multiple attractors. See e.g. Eric De Giuli and Camille Scalliet 2022 J. Phys. A: Math. Theor. 55 474002
(2) A class of models in which nonlinear reactions lead to growth and instability while diffusion (smoothing) tends to stabilize the system. Turing proposed one in 1952 to explain (among other things) how animals get stripes and spots; more recently the Gray-Scott model (1983) has been extensively studied. Calian extends the Gray-Scott model.