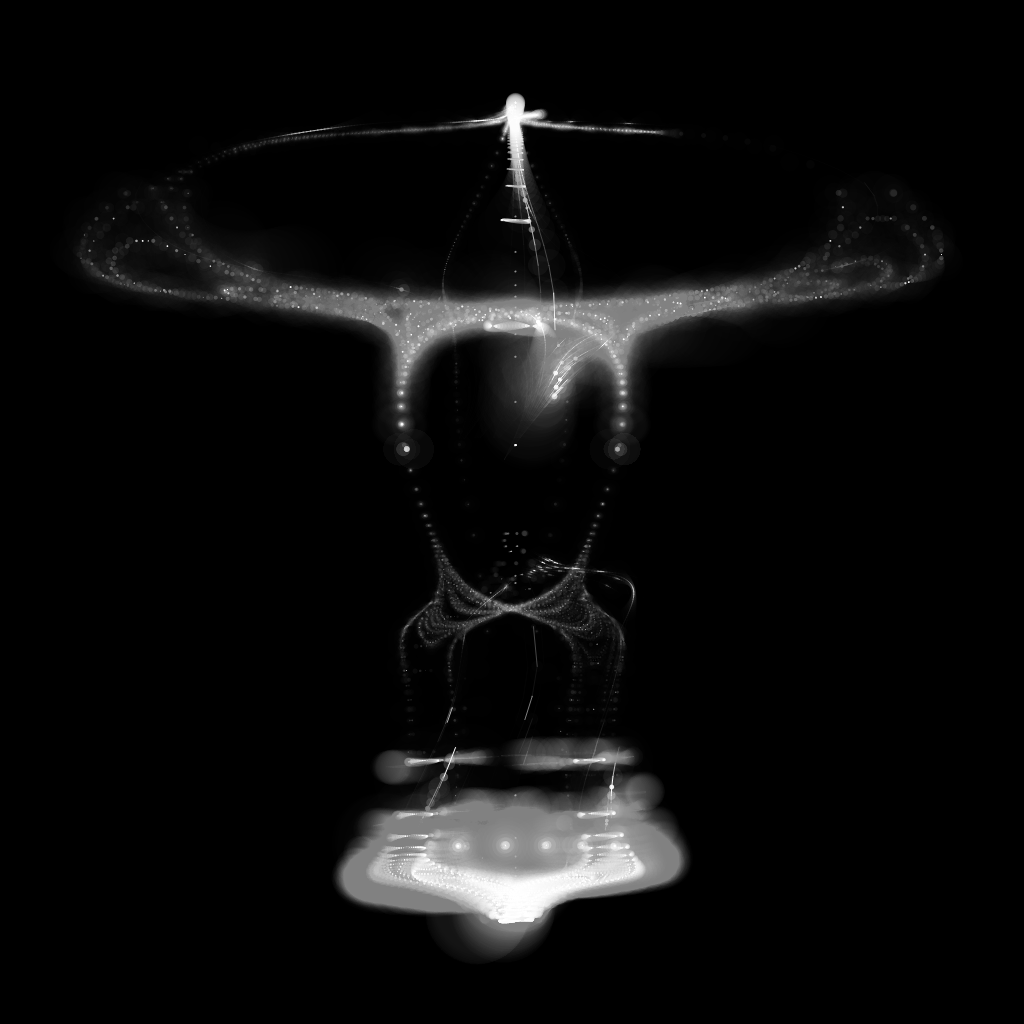
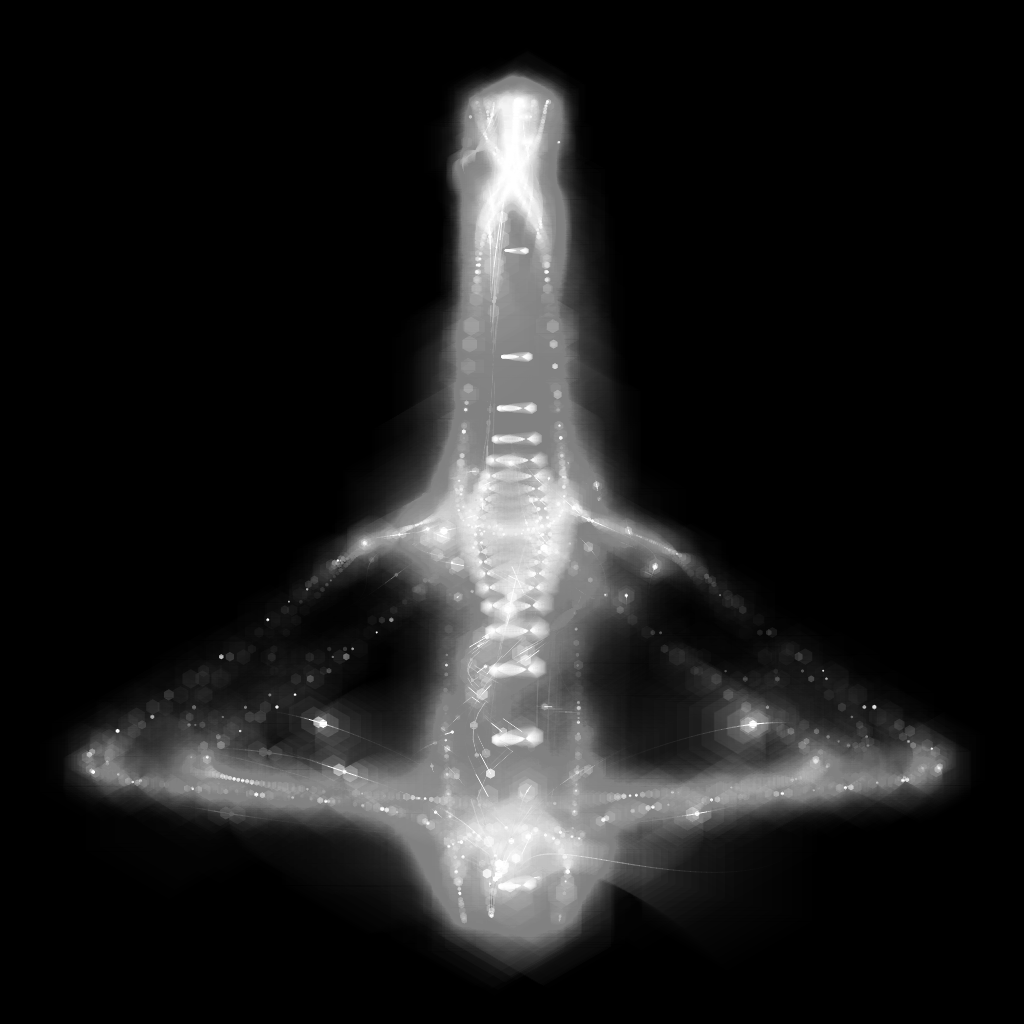
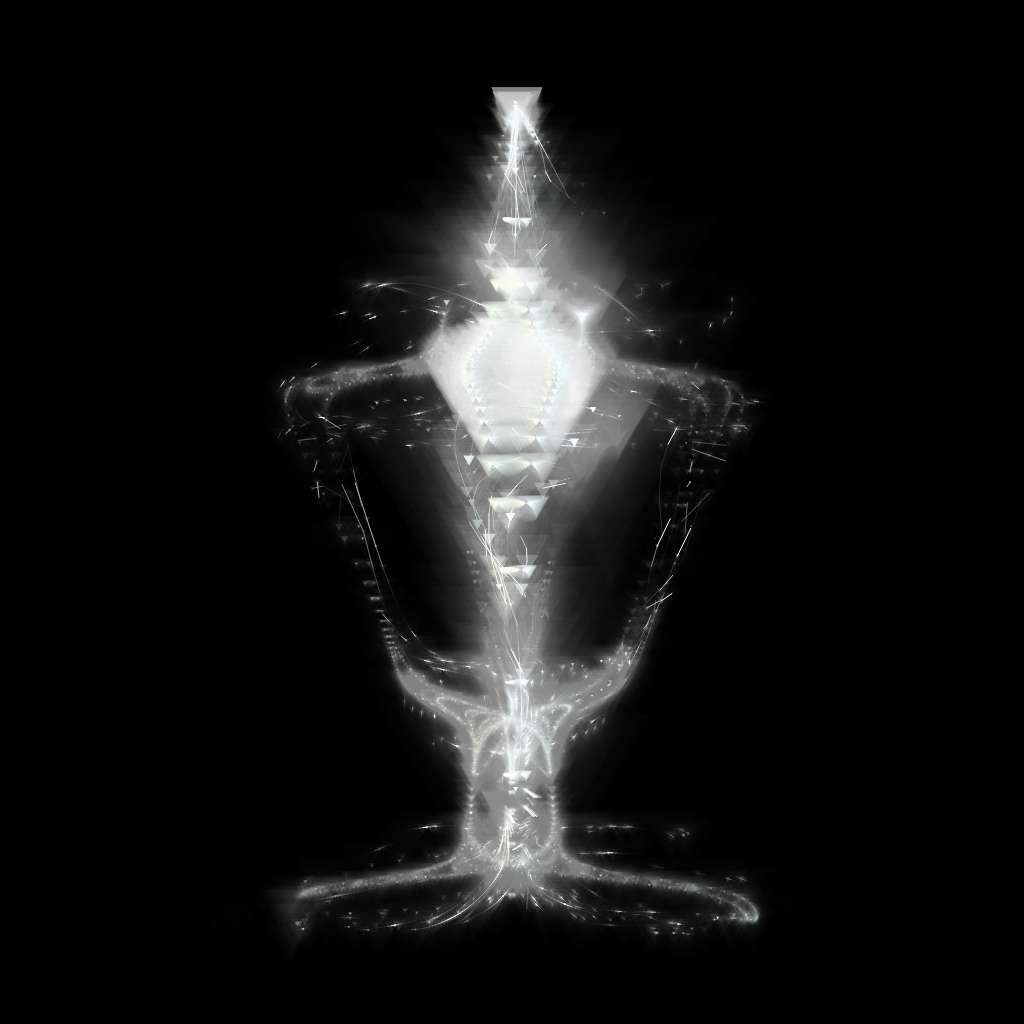
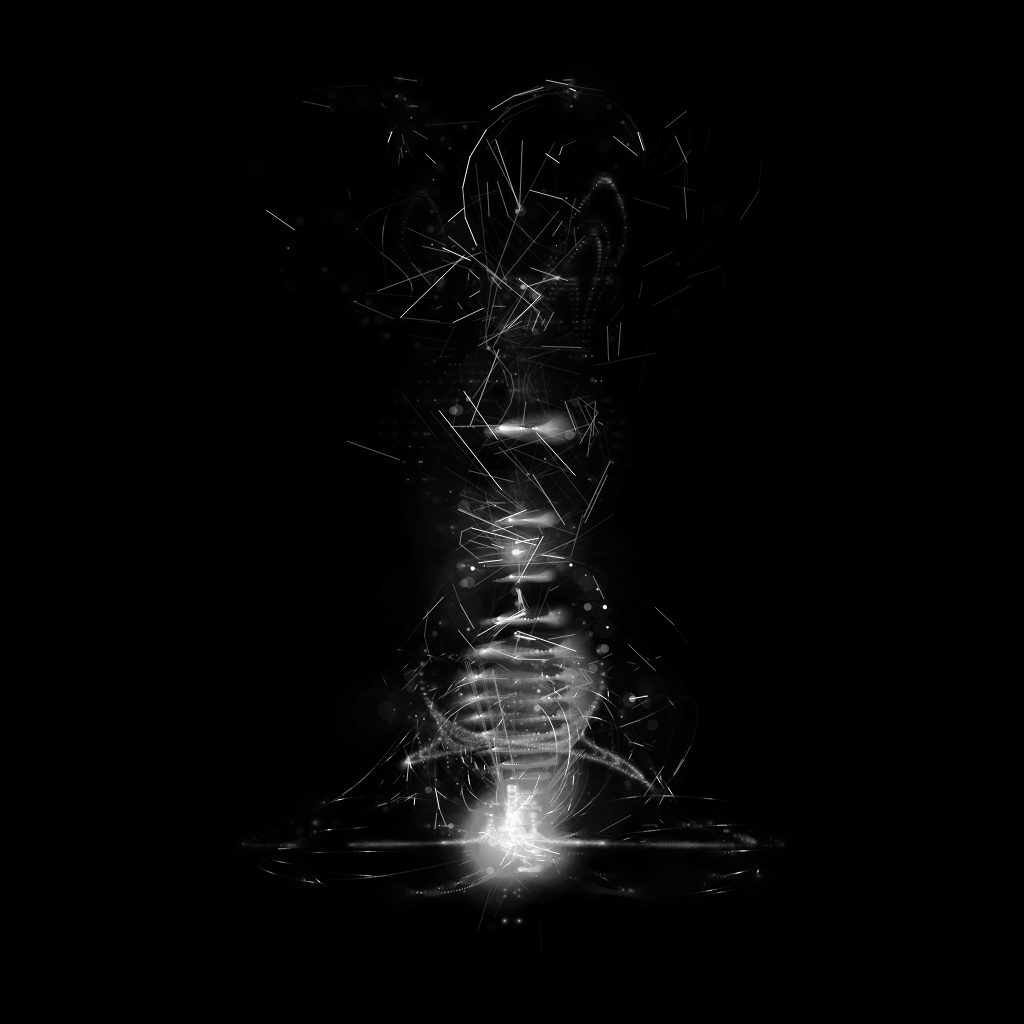
Spectral Beings are a series of 888 generative art works, rendered in javascript with the p5.js library, originally released on September 24, 2021. The 11kb code needed to create them is stored indefinitely on the ethereum blockchain.
The series is inspired by the uncomfortable thought that aliens are likely out there in the universe, but, by virtue of the great distances involved, utterly inaccessible to us. This dilemma presents an opportunity: to imagine an alien biology, following general principles that we establish on Earth.
In my day job as a theoretical physicist I work on the theory of living matter, using the fundamental laws of physics as constraints. But by night, I can take these same constraints and, through generative art, imagine the endless possibilities afforded by them.
Spectral beings explores the possibility of life made from light itself. The beings take a variety of forms..
[ from top, left to right: #160, #129, #85, #111, #181, #78, #196, #238, #197 ]
..but are all created from the same short code. [ the originals are fully periodic 4s films. clicking on an image above will take you to the corresponding film. ]
Each spectral being is uniquely specified by its seed value, generated on mint. This seed is a compressed key, inscrutable to the human eye but readable by the code itself. Much as our bodies use DNA to generate a suite of proteins, which carry functional significance, the seed value is parsed by the code to generate parameter values, which control the shape of each being. This article sketches this imagined alien genetic code. In the accompanying Appendix, I explain in more mathematical detail a key technique used in Spectral Beings, which should be of general interest for generative artists.
Each Spectral Being begins as a templated body form, with a number of antenna and body `lobes’. The details specifying this form are random and controlled by the seed. For example, the antenna angle, number of segments, relative head size, etc., are all variable. Here are some examples. alpha controls the relative head size, while each half-lobe is numbered.
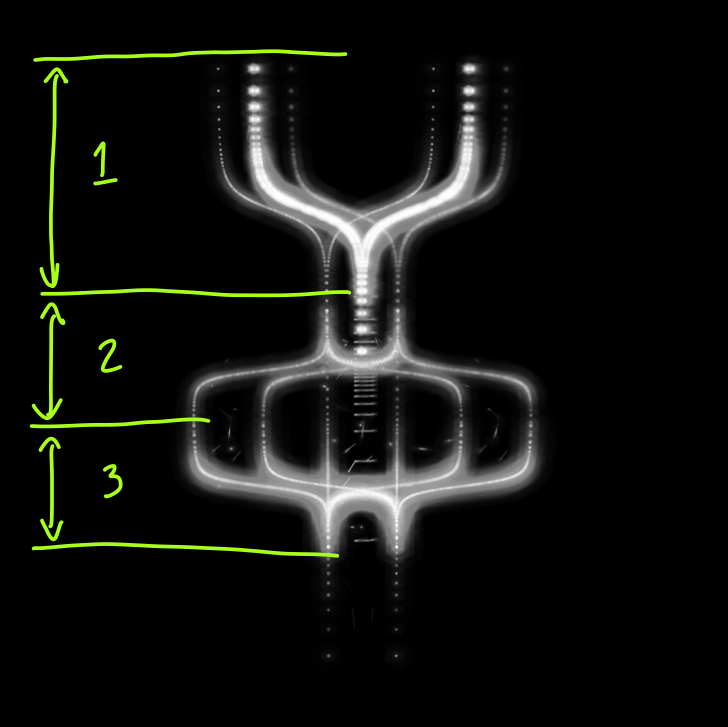
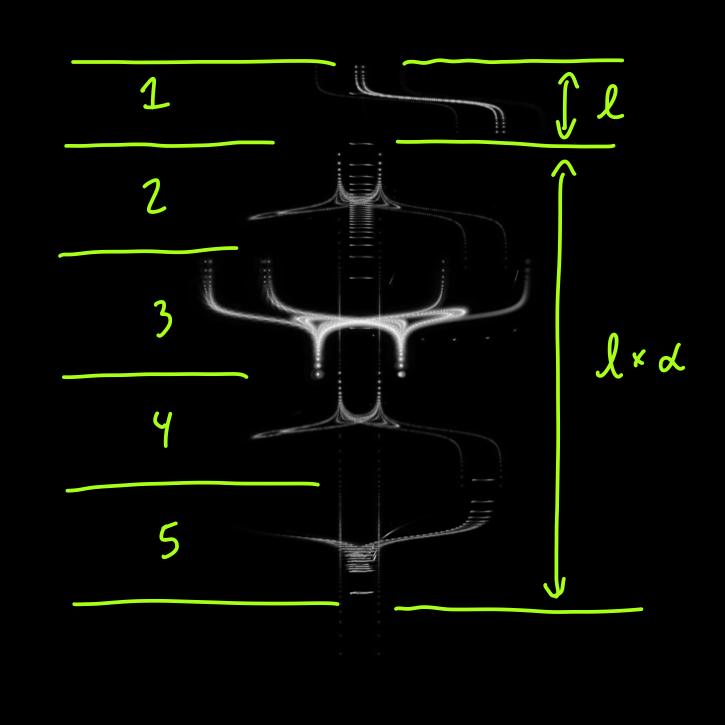
Although this already allows for a great variety of forms, the bodies are still just templates, with a roughly cylindrical shape. The beings are three dimensional, and at this point you can imagine a vertical y axis, and at each y, some radius r(y). Create a circle of that radius, and you’ll build up a hollow three dimensional form. Let’s fix the y axis to go from 0 to 100. Then, as we go from 0 to 100, the shape of the being is specified by r(0), r(1), and so on, up to r(100). (In reality, they are not perfectly symmetrical, but let’s ignore this complication)
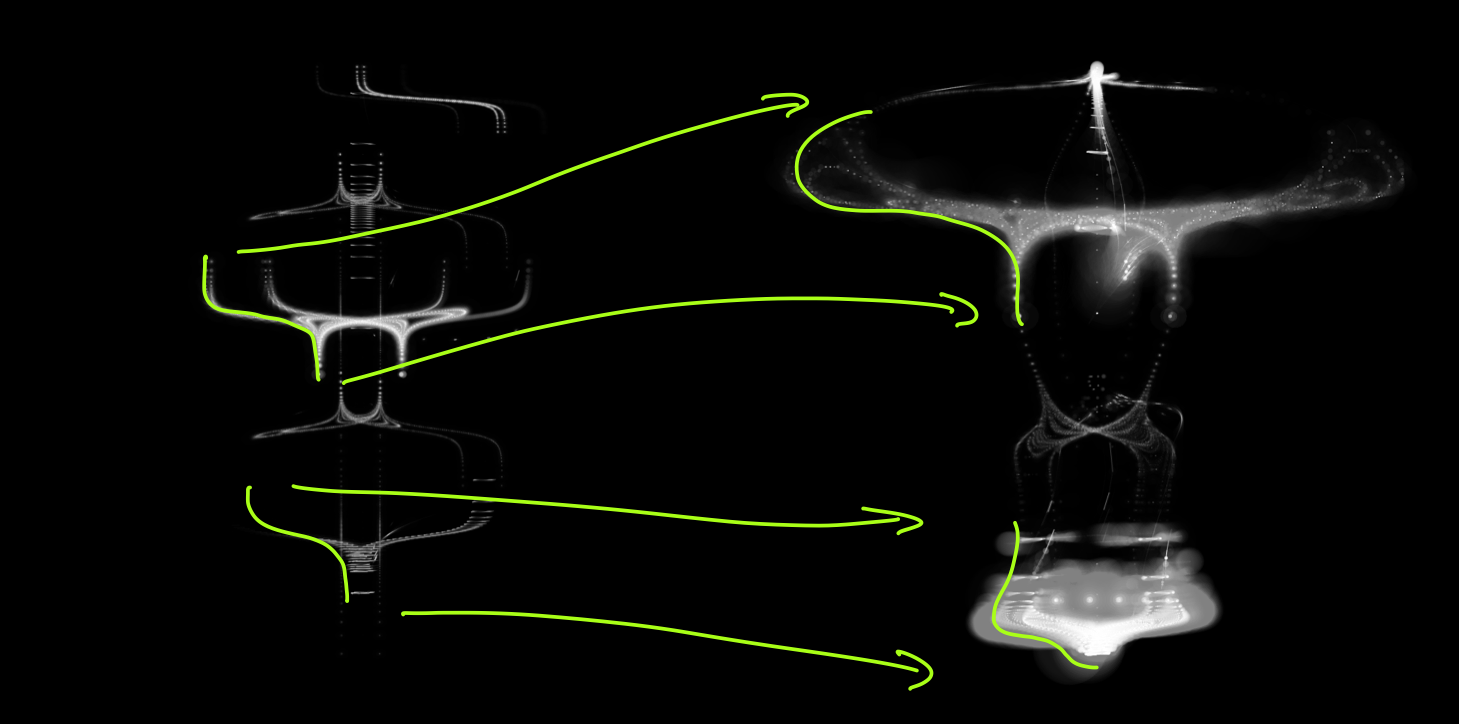
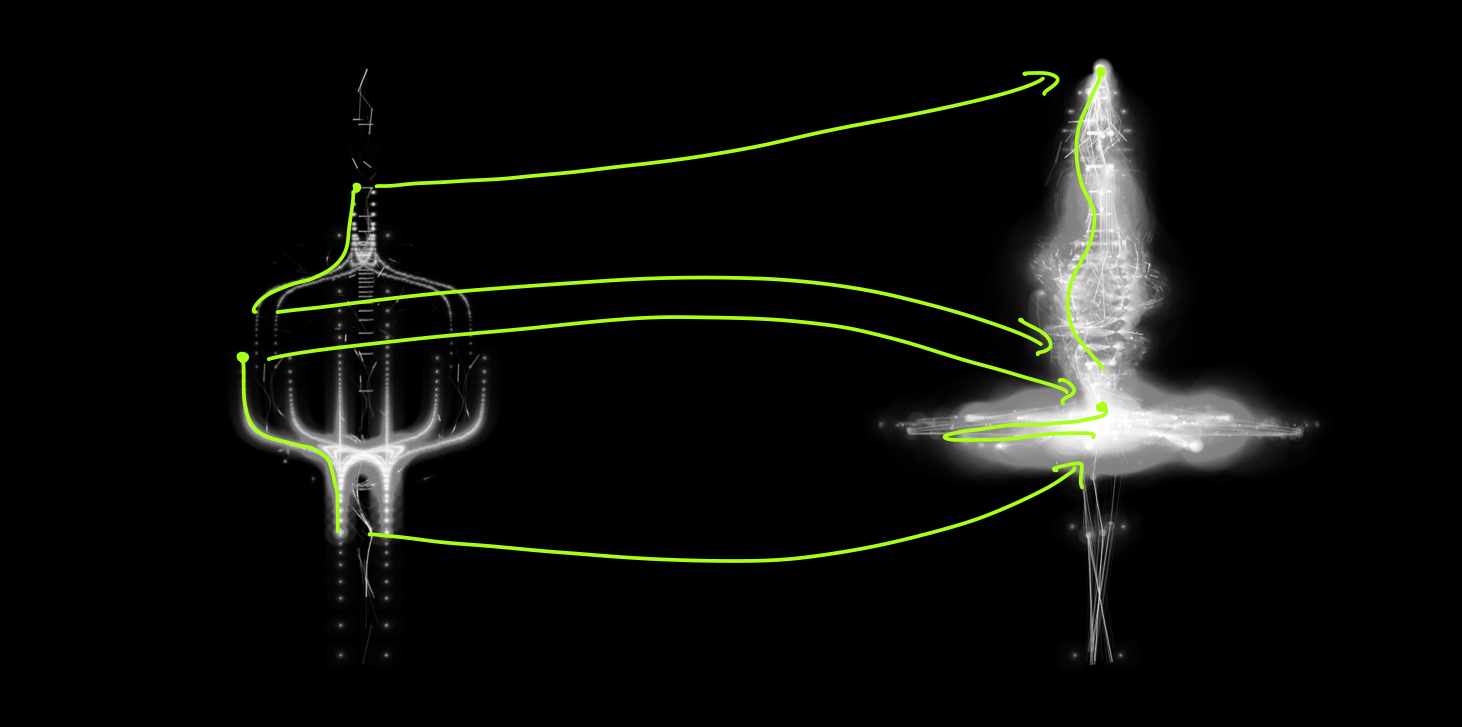
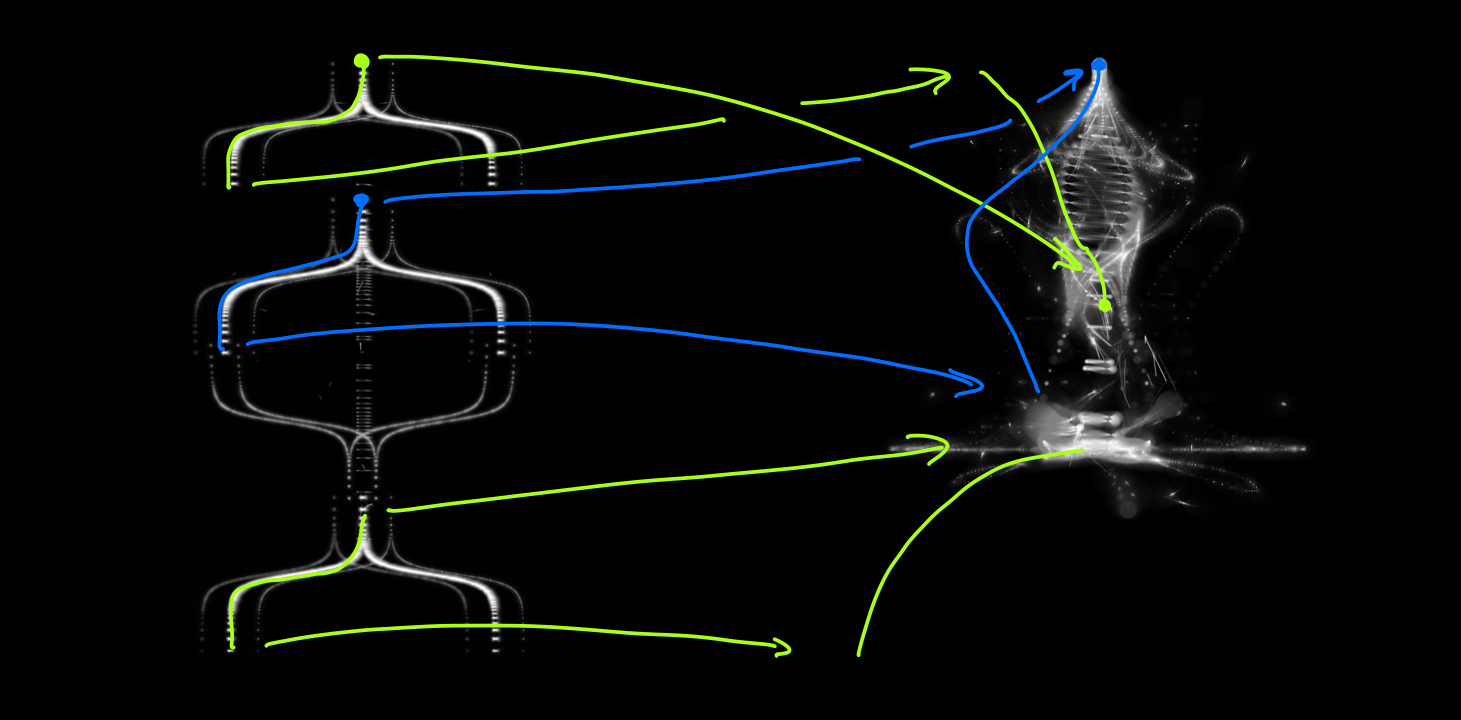
The next, crucial, step is a form of domain distortion. The key idea is simple: instead of plotting a point at y and r(y), we can pass the vertical and radial coordinates through functions f and g, and create a circle at f(y) with radius g(r(y)). If that sounds abstract, consider the following figure. The left side shows a templated form, with some segments marked out by green curves. Under the functions f and g, these curves get transformed, into the curves shown on the right side. The simplest class of domain distortion stretches or shrinks segments, but does not fold over shapes onto themselves. In this case the initial template is legible in the final body forms, but clearly the latter have character going much beyond their morphogenetic precursor.
By varying the domain distortion functions, a huge variety of forms can be created. For example, suppose we map a body segment so that the ‘waist’ touches the ‘knee’. Then we get a ballerina:
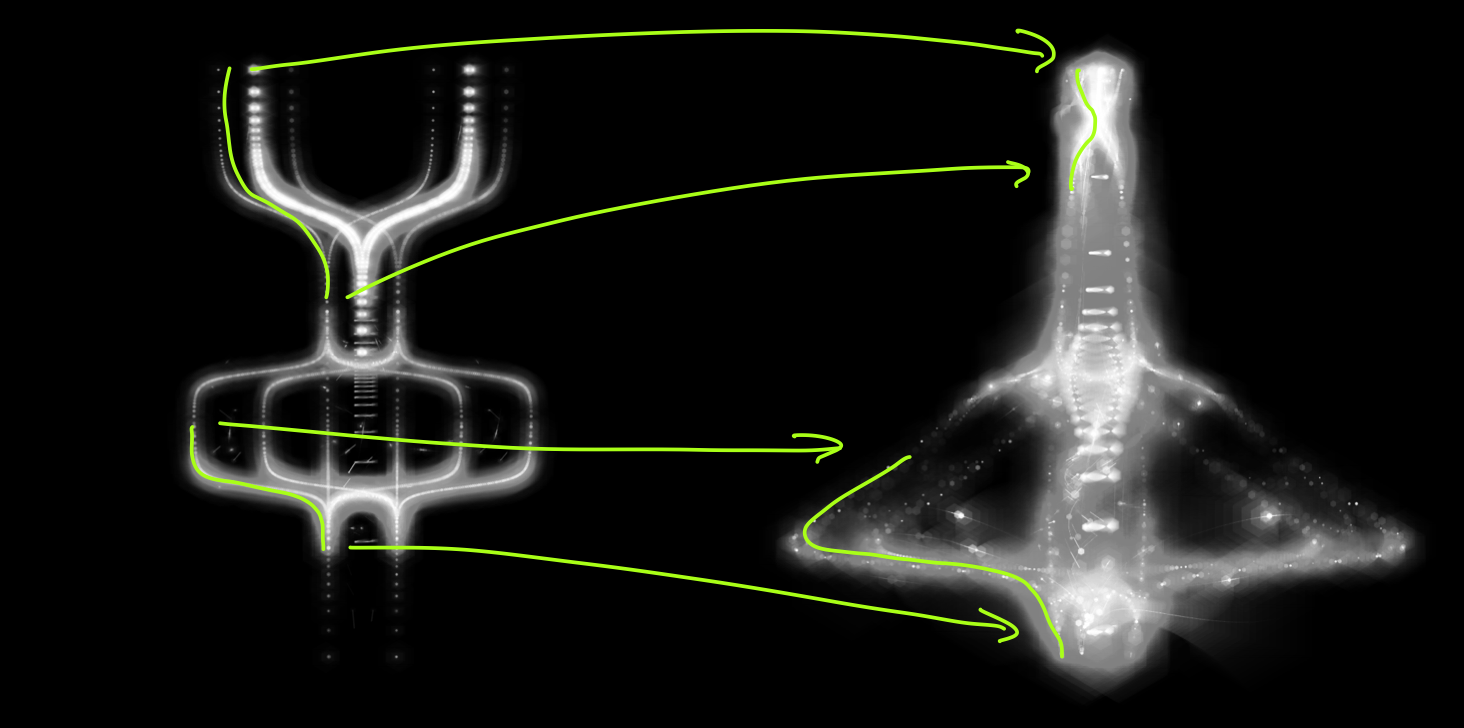
More intricate forms can be created by folding over body parts onto themselves. We can take what was the head, and map it onto the body core. Then the final form will have multiple ‘organs’, as in Spectral Beings 111 (left) or 160 (right):
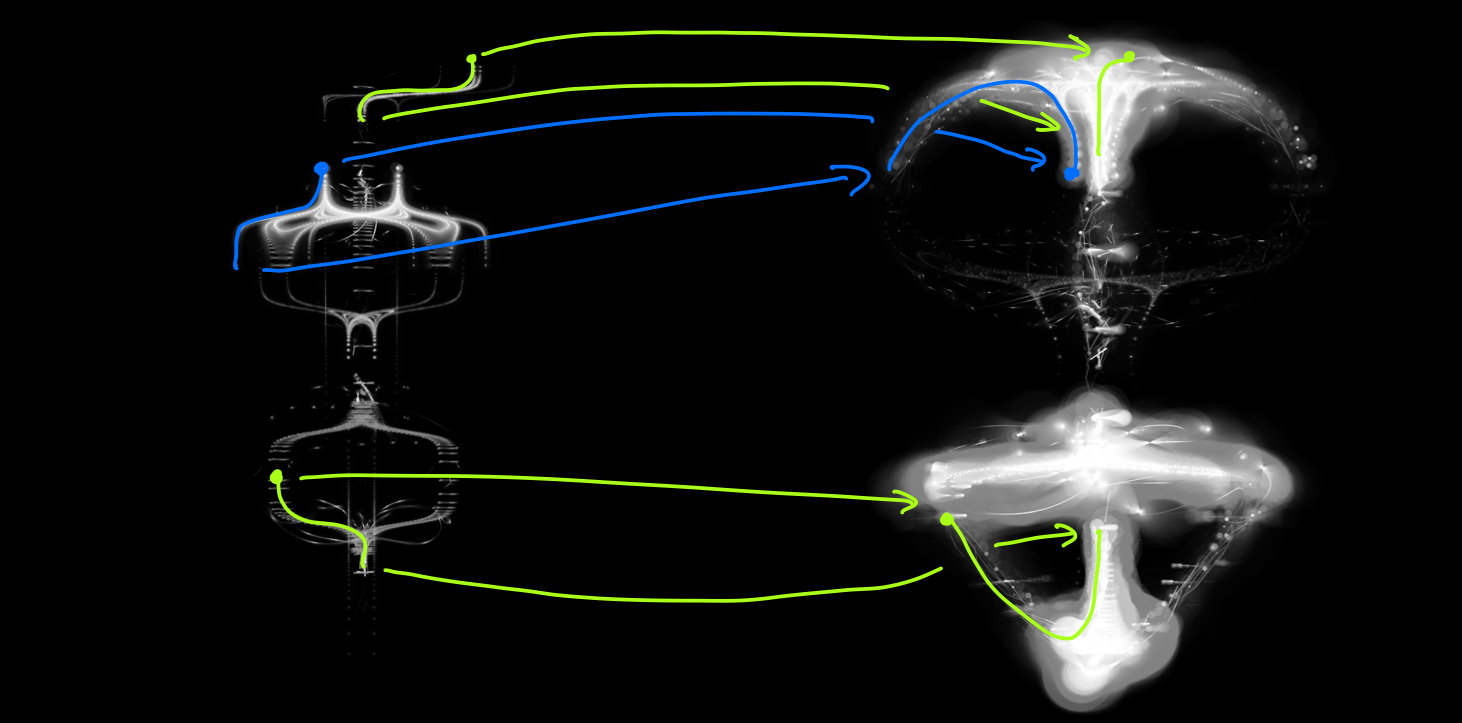
Similar forms of domain distortion are used by extant life in morphogenesis. For example, overexpression of a protein in the middle of the cell can cause a pinch -- one type of distortion -- that leads to cell division. Other expression patterns can lead to bulges, folds, stripes, appendages, and so on. Of course, while life in reality needs to follow the laws of physics, each morphogenetic phenomenon having a microscopic basis in chemical reactions, with generative art we can free ourselves of these limitations. Spectral Beings uses a large family of distortion functions chosen for their aesthetic consequences.
Domain distortion is a general tool, useful in many contexts. In milder forms, it can add nuance and variety to simple shapes, while in more extreme versions, it offers endless possibilities for morphogenesis, limited only by the creativity of the artist.
Appendix
Here we explain domain distortion in more mathematical terms. For simplicity, consider the one dimensional case. We write y for the initial coordinate, and Y for the transformed one. Y = f(y) where f is the domain distortion function. How does the form of f control the resulting shape? Consider first the trivial case f(y) = y. Then Y=y and there is no distortion at all. Now let us add complexity. f(y) = c y, where c is some constant, just scales y by a constant factor c. f(y) = y + a, where a is some constant, shifts y by a constant factor a. We can, of course, combine these: f(y) = c y + a performs both a shift and a scaling. But these examples are hardly deserving of the name distortion. To go further, we need to consider nonlinear functions f.
An endless family of functions are possible. In Spectral Beings, the domain distortion functions are chosen from trigonometric functions, like the sine function. To understand why this family is interesting, consider what happens when f(y) has a local maximum, say at y*. Let f(y*) = Y*. Then for y a little bit smaller than y*, we have f(y) < Y. And similarly for y a little bit larger than y*, we also have f(y) < Y. Close enough to y*, for each point y1 we can find another point y2 on the other side of y* that maps to the same value Y1. Thus this distortion creates a fold. A similar argument applies to local minima, which also create folds.
With the trigonometric functions, we can create a variable number of folds, just by controlling n in the expression f(y) = sin(n y). If y goes from 0 to 2 Pi, then when n=1 we get one local maximum and one local minimum: two folds. But if n=2, then we get 4 folds. And so on.
Moreover, we can also add a phase to the function: f(y) = sin(n y + b). By varying b, we control where the folds occur. Do they start at the head, or somewhere further down?
Again, all these complexities can be combined. In Spectral Beings, both the vertical coordinates y and the radial coordinates r are distorted. The resulting functions are much harder to visualize, although the same mathematical principles apply.